Lesson 15

Strength in numbers

Let me see: four times five is twelve, and four times six is thirteen, and four times seven is fourteen—oh dear! I shall never get to twenty at this rate!
Read by Guy Swann.

Numbers are an essential part of our everyday life. Large numbers, however, aren’t something most of us are too familiar with. The largest numbers we might encounter in everyday life are in the range of millions, billions, or trillions. We might read about millions of people in poverty, billions of dollars spent on bank bailouts, and trillions of national debt. Even though it’s hard to make sense of these headlines, we are somewhat comfortable with the size of those numbers.

Although we might seem comfortable with billions and trillions, our intuition already starts to fail with numbers of this magnitude. Do you have an intuition how long you would have to wait for a million/billion/trillion seconds to pass? If you are anything like me, you are lost without actually crunching the numbers.

Let’s take a closer look at this example: the difference between each is an increase by three orders of magnitude: 10⁶, 10âč, 10ÂčÂČ. Thinking about seconds is not very useful, so let’s translate this into something we can wrap our head around:

  • 10⁶: One million seconds was 1Âœ weeks ago.
  • 10âč: One billion seconds was almost 32 years ago.
  • 10ÂčÂČ: One trillion seconds ago Manhattan was covered under a thick layer of ice.
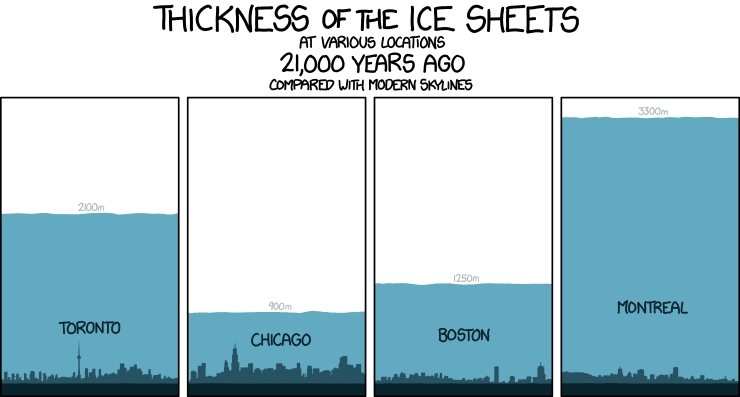
About 1 trillion seconds ago. Source: xkcd #1225

As soon as we enter the beyond-astronomical realm of modern cryptography, our intuition fails catastrophically. Bitcoin is built around large numbers and the virtual impossibility of guessing them. These numbers are way, way larger than anything we might encounter in day-to-day life. Many orders of magnitude larger. Understanding how large these numbers truly are is essential to understanding Bitcoin as a whole.

Let’s take SHA-256, one of the hash functions used in Bitcoin, as a concrete example. It is only natural to think about 256 bits as “two hundred fifty-six,” which isn’t a large number at all. However, the number in SHA-256 is talking about orders of magnitude — something our brains are not well-equipped to deal with.

While bit length is a convenient metric, the true meaning of 256-bit security is lost in translation. Similar to the millions (10⁶) and billions (10âč) above, the number in SHA-256 is about orders of magnitude (2ÂČ⁔⁶).

So, how strong is SHA-256, exactly?

“SHA-256 is very strong. It’s not like the incremental step from MD5 to SHA1. It can last several decades unless there’s some massive breakthrough attack.” Satoshi Nakamoto

Let’s spell things out. 2ÂČ⁔⁶ equals the following number:

115 quattuorvigintillion 792 trevigintillion 89 duovigintillion 237 unvigintillion 316 vigintillion 195 novemdecillion 423 octodecillion 570 septendecillion 985 sexdecillion 8 quindecillion 687 quattuordecillion 907 tredecillion 853 duodecillion 269 undecillion 984 decillion 665 nonillion 640 octillion 564 septillion 39 sextillion 457 quintillion 584 quadrillion 7 trillion 913 billion 129 million 639 thousand 936.

That’s a lot of nonillions! Wrapping your head around this number is pretty much impossible. There is nothing in the physical universe to compare it to. It is far larger than the number of atoms in the observable universe. The human brain simply isn’t made to make sense of it.

One of the best visualizations of the true strength of SHA-256 is the following video by Grant Sanderson. Aptly named “How secure is 256 bit security?” it beautifully shows how large a 256-bit space is. Do yourself a favor and take the five minutes to watch it. As all other 3Blue1Brown videos it is not only fascinating but also exceptionally well made. Warning: You might fall down a math rabbit hole.

Answer: Pretty secure.

Bruce Schneier used the physical limits of computation to put this number into perspective: even if we could build an optimal computer, which would use any provided energy to flip bits perfectly, build a Dyson sphere around our sun, and let it run for 100 billion billion years, we would still only have a 25% chance to find a needle in a 256-bit haystack.

“These numbers have nothing to do with the technology of the devices; they are the maximums that thermodynamics will allow. And they strongly imply that brute-force attacks against 256-bit keys will be infeasible until computers are built from something other than matter and occupy something other than space.” Bruce Schneier

It is hard to overstate the profoundness of this. Strong cryptography inverts the power-balance of the physical world we are so used to. Unbreakable things do not exist in the real world. Apply enough force, and you will be able to open any door, box, or treasure chest.

Bitcoin’s treasure chest is very different. It is secured by strong cryptography, which does not give way to brute force. And as long as the underlying mathematical assumptions hold, brute force is all we have. Granted, there is also the option of a global $5 wrench attack. But torture won’t work for all Bitcoin addresses, and the cryptographic walls of Bitcoin will defeat brute force attacks. Even if you come at it with the force of a thousand suns. Literally.

This fact and its implications were poignantly summarized in the call to cryptographic arms: “No amount of coercive force will ever solve a math problem.”

“It isn’t obvious that the world had to work this way. But somehow the universe smiles on encryption.” Julian Assange

Nobody yet knows for sure if the universe’s smile is genuine or not. It is possible that our assumption of mathematical asymmetries is wrong and we find that P actually equals NP, or we find surprisingly quick solutions to specific problems which we currently assume to be hard. If that should be the case, cryptography as we know it will cease to exist, and the implications would most likely change the world beyond recognition.

“Vires in Numeris” = “Strength in Numbers” epii

Vires in numeris is not only a catchy motto used by bitcoiners. The realization that there is an unfathomable strength to be found in numbers is a profound one. Understanding this, and the inversion of existing power balances which it enables changed my view of the world and the future which lies ahead of us.

One direct result of this is the fact that you don’t have to ask anyone for permission to participate in Bitcoin. There is no page to sign up, no company in charge, no government agency to send application forms to. Simply generate a large number and you are pretty much good to go. The central authority of account creation is mathematics. And God only knows who is in charge of that.

Elliptic curve examples (cc-by-sa Emmanuel Boutet)

Bitcoin is built upon our best understanding of reality. While there are still many open problems in physics, computer science, and mathematics, we are pretty sure about some things. That there is an asymmetry between finding solutions and validating the correctness of these solutions is one such thing. That computation needs energy is another one. In other words: finding a needle in a haystack is harder than checking if the pointy thing in your hand is indeed a needle or not. And finding the needle takes work.

The vastness of Bitcoin’s address space is truly mind-boggling. The number of private keys even more so. It is fascinating how much of our modern world boils down to the improbability of finding a needle in an unfathomably large haystack. I am now more aware of this fact than ever.

Bitcoin taught me that there is strength in numbers.

    Down the Rabbit Hole